Tree

Tree（樹）是一種資料結構，是具有樹狀結構性質的資料集合，根朝上，而葉朝下，它具有以下的特點：

• 每個節點都只有有限個子節點或無子節點
• 沒有父節點的節點稱為根節點
• 每一個非根節點有且只有一個父節點
• 除了根節點外，每個子節點可以分為多個不相交的子樹
• 樹裡面沒有環路(cycle)，而環是一條只有第一個和最後一個頂點重複的非空路徑

mutableListOf 是 Kotlin 程式語言中的一個函數，用於建立一個可變的列表（mutable list）。
在 Kotlin 中，列表是一種用於存儲一組元素的數據結構，可變列表與不可變列表（immutable list）的區別在於，可變列表允許在創建後添加、刪除或修改其中的元素，而不可變列表則不允許修改其內容。

// Kotlin implement tree data structure
class TreeNode<T>(val value: T) {
    var children: MutableList<TreeNode<T>> = mutableListOf()
    fun add(child: TreeNode<T>) = children.add(child)
    fun remove(child: TreeNode<T>) = children.remove(child)
    override fun toString(): String {
        var s = "${value}"
        if (!children.isEmpty()) {
            s += " {" + children.map { it.toString() }.joinToString(", ") + " }"
        }
        return s
    }
}

// Tree overview
// beverages
// ├── hot
// │   ├── tea
// │   │   ├── black tea
// │   │   ├── green tea
// │   │   └── chai tea
// │   ├── coffee (removed)
// │   └── cocoa
// └── cold
//     ├── soda
//     │   ├── ginger ale
//     │   └── bitter lemon
//     └── milk


fun main() {
    val tree = TreeNode("beverages")
    val hot = TreeNode("hot")
    val cold = TreeNode("cold")
    val tea = TreeNode("tea")
    val coffee = TreeNode("coffee")
    val cocoa = TreeNode("cocoa")
    val blackTea = TreeNode("black tea")
    val greenTea = TreeNode("green tea")
    val chaiTea = TreeNode("chai tea")
    val soda = TreeNode("soda")
    val milk = TreeNode("milk")
    val gingerAle = TreeNode("ginger ale")
    val bitterLemon = TreeNode("bitter lemon")
    tree.add(hot)
    tree.add(cold)
    hot.add(tea)
    hot.add(coffee)
    hot.add(cocoa)
    cold.add(soda)
    cold.add(milk)
    tea.add(blackTea)
    tea.add(greenTea)
    tea.add(chaiTea)
    soda.add(gingerAle)
    soda.add(bitterLemon)
    println(tree)
    // remove an item
    hot.remove(coffee)
    println(tree)
}

我們預設新加入的節點都是樹的葉子節點，也就是說，新加入的節點沒有子節點。

且由左至右加入節點，也就是說，新加入的節點會成為同一層的最右節點。

Graph

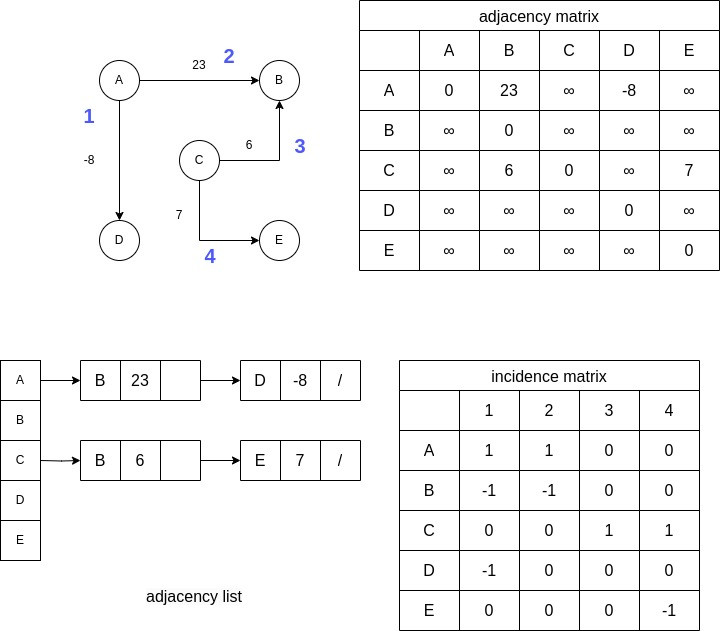
Graph（圖）是一種抽象數據類型，用於實現數學中圖論的無向圖和有向圖的概念。

而圖我們可以呈現的方式主要有三種：

• Adjacency list（鄰接表）
• Adjacency matrix（鄰接矩陣）
• Incidence matrix（關聯矩陣）

// Kotlin implement graph data structure
// The graph has directed edges, meaning that the edge points from one node to another.
class Graph<T> {
    private val nodes: MutableList<Node<T>> = mutableListOf()
    fun addNode(node: Node<T>) = nodes.add(node)
    fun removeNode(node: Node<T>) = nodes.remove(node)
    fun addEdge(source: Node<T>, destination: Node<T>) {
        if (!nodes.contains(source) || !nodes.contains(destination)) {
            throw Exception("Source and Destination nodes must be part of graph")
        }
        val edge = Edge(source, destination)
        source.addEdge(edge)
    }
    fun removeEdge(source: Node<T>, destination: Node<T>) {
        if (!nodes.contains(source) || !nodes.contains(destination)) {
            throw Exception("Source and Destination nodes must be part of graph")
        }
        val edge = Edge(source, destination)
        source.removeEdge(edge)
    }
    fun print() {
        nodes.forEach { node ->
            node.edges.forEach { edge ->
                println("${edge.source.value} -> ${edge.destination.value}")
            }
        }
    }
}

class Node<T>(val value: T) {
    var edges: MutableList<Edge<T>> = mutableListOf()
    fun addEdge(edge: Edge<T>) = edges.add(edge)
    fun removeEdge(edge: Edge<T>) = edges.remove(edge)
}

class Edge<T>(val source: Node<T>, val destination: Node<T>) {
    override fun equals(other: Any?): Boolean {
        if (other !is Edge<*>) {
            return false
        }
        return source == other.source && destination == other.destination
    }
}

fun main() {
    val graph = Graph<String>()
    val nodeA = Node("A")
    val nodeB = Node("B")
    val nodeC = Node("C")
    val nodeD = Node("D")
    val nodeE = Node("E")
    val nodeF = Node("F")
    val nodeG = Node("G")
    val nodeH = Node("H")
    val nodeI = Node("I")
    graph.addNode(nodeA)
    graph.addNode(nodeB)
    graph.addNode(nodeC)
    graph.addNode(nodeD)
    graph.addNode(nodeE)
    graph.addNode(nodeF)
    graph.addNode(nodeG)
    graph.addNode(nodeH)
    graph.addNode(nodeI)
    graph.addEdge(nodeA, nodeB)
    graph.addEdge(nodeA, nodeC)
    graph.addEdge(nodeA, nodeD)
    graph.addEdge(nodeB, nodeE)
    graph.addEdge(nodeB, nodeF)
    graph.addEdge(nodeC, nodeG)
    graph.addEdge(nodeC, nodeH)
    graph.addEdge(nodeD, nodeI)
    graph.print()
    // A -> B
    // A -> C
    // A -> D
    // B -> E
    // B -> F
    // C -> G
    // C -> H
    // D -> I
    graph.removeEdge(nodeA, nodeB)
    graph.removeEdge(nodeA, nodeC)
    graph.removeEdge(nodeA, nodeD)
    graph.removeEdge(nodeB, nodeE)
    graph.removeEdge(nodeB, nodeF)
    graph.removeEdge(nodeC, nodeG)
    graph.removeEdge(nodeC, nodeH)
    graph.removeEdge(nodeD, nodeI)
    graph.print()
    // graph.removeNode(nodeA)
    // graph.removeNode(nodeB)
    // graph.removeNode(nodeC)
    // graph.removeNode(nodeD)
    // graph.removeNode(nodeE)
    // graph.removeNode(nodeF)
    // graph.removeNode(nodeG)
    // graph.removeNode(nodeH)
    // graph.removeNode(nodeI)
    // graph.print()
}

Terminal 輸出

A -> B
A -> C
A -> D
B -> E
B -> F
C -> G
C -> H
D -> I

所有 Code 可以在 Github 找到 ～

明天要開始重點部份，演算法實做了！！！
首先從 Sorting 開始

Reference

• What is a tree data structure?